ImageProcessing| Histogram Equalization, CLAHE
Histogram Equalization, CLAHE 이해하기
김동근 교수님, 파이썬으로 배우는 OpenCV 위키피디아 Histogram Equalization 선형 보간법(linear, bilinear, trilinear interpolation) linear, bilinear, inetrpolation 개념 정리
Histogram
히스토그램은 관찰 데이터의 빈도수(frequency)를 막대그래프로 표시한 것으로 데이터의 확률분포함수를 추정, 히스토그램은 영상 화소의 분포에 중요한 정보
Histogram Equalization
히스토그램 평활화는 입력 영상의 화소값에 대하여 누적 분포 함수를 변환 함수로 사용하여 출력 영상의 화소값을 계산하는 영상개선(image enhancement) 방법
화소값의 범위가 좁은 저대비(low contrast) 입력 영상을 화소값의 범위가 넓은 고대비(high contrast) 출력 영상을 얻음
즉, 밝기값이 몰려있어 어둡거나 또는 밝거나 한 영상을 평활화하면 더욱 선명한 영상을 얻음
컬러 영상의 히스토그램 평활화는 HSV, YCrCb 등의 컬러 모델로 변환한 다음, 밝기 값 채널(V, Y)에 히스토그램 평활화를 적용한 후에 BGR 컬러로 변환
히스토그램 평활화 알고리즘
- src 영상에서 256개의 빈에 히스토그램 hist를 계산
- hist의 누적합계 cdf를 계산
- cdf에서 0을 제외한 최소값(cdf_min)과 최대값(cdf_max)를 계산
- 변환표 T를 계산
일반적인 평활화 공식
- cdf_min은 0을 제외, M: 너비, L: 보통 256의 수
예를 들어 78의 cdf는 46이면
배열의 히스토그램 평활화(코드)
hist, bins = np.histogram(src.flatten(), 256, [0, 256])
cdf = hist.cumsum()
cdf_m = np.ma.masked_equal(cdf, 0) # cdf에서 0을 True로 마스킹
T = (cdf_m - cdf_m.min()) * 255 / (cdf_m.max() - cdf_m.min())
T = np.ma.filled(T, 0).astype('unit8') # 마스킹을 0으로 채우기
dst2 = T[src] # dst2 = dst
그레이스케일 히스토그램 평활화(코드)
cv2.imread를 grayscale로 받고, equalizeHist
컬러 영상의 히스토그램 평활화(코드)
HSV/YCrCb로 변환 후 V, Y에 평활화 적용 후 BGR
hsv = cv2.cvtColor(src, cv2.COLOR_BGR2HSV)
h, s, v = cv2.split(hsv)
# YCrCb의 경우 y가 밝기 채널
v2 = cv2.equlizaeHist(v) # 밝기
hsv2 = cv2.merge([h, s, v2])
번외: HSV, YCrCb
HSV
- Hue(색조; 0~179)
- Saturation(채도; 맑고 탁한 정도; 0~255)
- Value(명도; 밝기; 0~255)
YCrCb(YCC)
- Y(Luminance; 밝기)
- Cr(Chroma red; 적색 색차(빨간색 - Y))
- Cb(Chroma blue; 청색 색차(파란색 - Y))
선형 보간법(interpolation)
- interpolation: 알려진 지점의 값 사이에 위치한 값을 알려진 값으로부터 추정 <-> extrapolation: 알려진 사이의 값이 아닌 범위를 벗어난 외부의 위치에서의 값을 추정
1D Linear interpolation
두 지점을 보간하는 방법: polynomial, spline 등 그중에 linear는 두 지점 사이의 값을 추정할 때 직선 거리에 따라 선형적으로 결정
- 첫 번째 지점 x1의 데이터 값: f(x1)
- 두 번째 지점 x2의 데이터 값: f(x2)
- 그 사이 임의의 지점: f(x)
를 선형 보간법을 사용한다면 다음과 같이 계산
- d1: x에서 x1까지의 거리
- d2: x에서 x2까지의 거리
를 정리하면 아래와 같음
거리의 비를 합이 1이 되도록 정규화한다면 더 단순화도 가능
Bilinear Interpolation(양선형 보간, 쌍선형 보간법, 이중선형 보간법)
- 1차원에서 2차원으로 확장
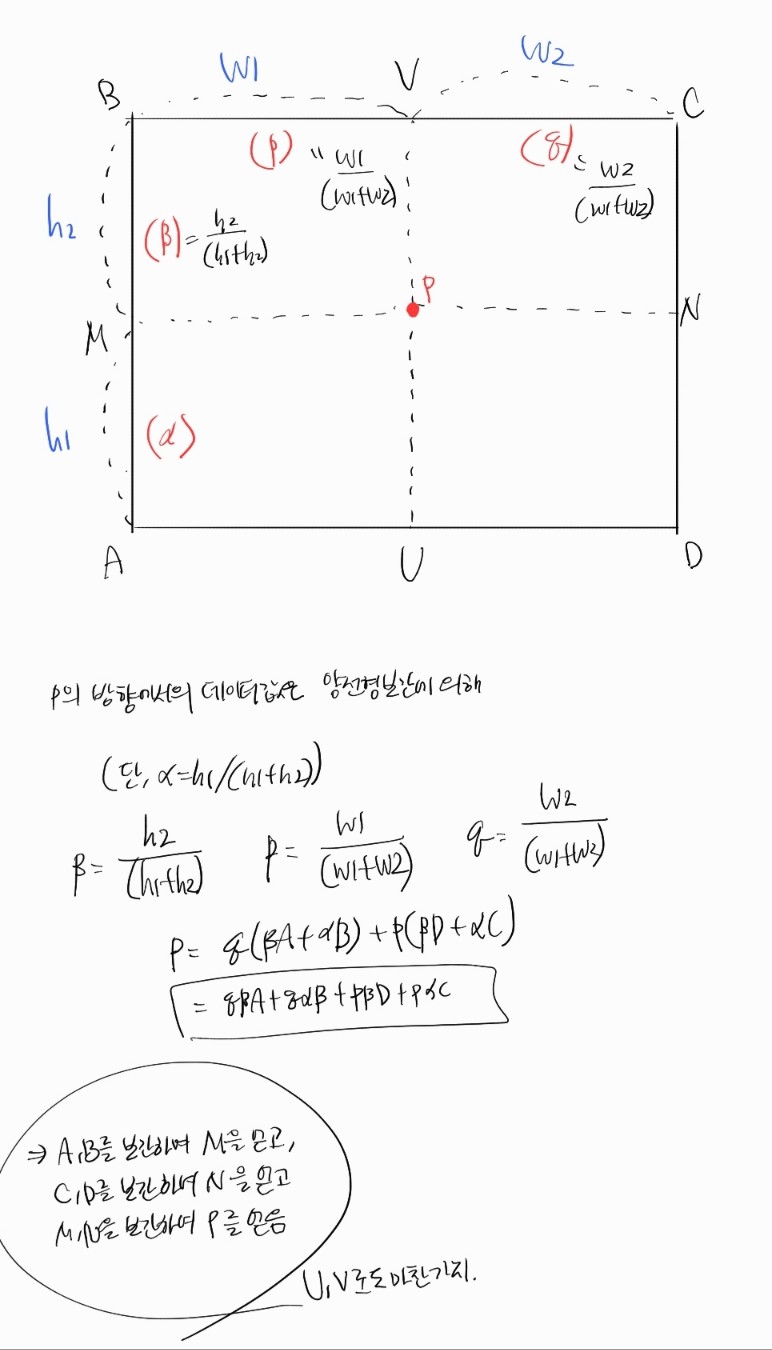
- 직사각형의 네 꼭지점의 값이 주어졌을 때, 사각형의 변 및 내부의 임의의 점에서의 값을 추정하는 문제
Trilinear Interpolation(삼선형 보간법)
- 1차원에서 3차원으로 확장
히스토그램의 보간
- 히스토그램 변환작업시 bin의 크기에 따라 계단현상이 발생
- 이를 완화시키기 위한 보간 방법이 주로 사용되는데
- HOG: gradient 방향 히스토그램을 구할 때 trilinear interpolation 방법이 적용
2D 히스토그램을 생성하는 경우
하나의 입력 데이터에 대해서 해당 데이터와 가장 가까운 인접한 4개의 bin 값을 bilinear interpolation 방식에 의해 증가시킴
추출한 feature 값이 (f, g)이고 (f, g)와 가장 가까운 서로 인접한 4개의 히스토그램 bin을 (f1, g1), (f2, g1), (f1, g2), (f2, g2), f와 f1의 거리를 d1, f와 f2의 거리를 d2, g와 g1과의 거리를 k1, g2와의 거리를 k2라 하면 각각의 bin 값들은
- (f1, g1) : d2/(d1+d2) * k2/(k1+k2) 만큼 증가
- (f1, g2) : d2/(d1+d2) * k1/(k1+k2) 만큼 증가
- (f2, g1) : d1/(d1+d2) * k2/(k1+k2) 만큼 증가
- (f2, g2) : d1/(d1+d2) * k1/(k1+k2) 만큼 증가
구현 코드
def interpolate(sub_image, UL, UR, BL, BR):
dst = np.zeros(sub_image.shape)
sY, sX = sub_image.shape
for y in range(sY):
invY = sY - y
for x in range(sX):
invX = sX - x
val = sub_image[y, x].astype(int)
dst[y, x] = np.floor(
(invY * (invX * UL[val] + x * UR[val]) +
y * (invX * BL[val] + x * BR[val])) / area)
return dst
- LUT: 변환 테이블
- (UL, UR) 상단 두 LUT 사이 선형보간
- (BL, BR) 하단 두 LUT 사이 선형보간
- 그리고 위아래 두 값을 다시 y 기준으로 보간
- area = sX * sY로 보간 가중치 정규화
CLAHE
의료 영상에서
- 의료 영상은 포맷 외에도 조명 및 대비 문제로 인해 시각적 이해가 어려운데 이를 개선하기 위해서 히스토그램 평활화 과정 적용
- 주로 이미지의 대비를 향상시키기 위해 사용하며 Histogram Equalization은 원본 전체 이미지에 적용
CLAHE는 대비를 제한하고, 영상을 타일로 나누어 각 타일별로 히스토그램을 평활화하고, 양선형 보간
타일의 히스토그램에서 대비 제한(contrast limit)보다 큰 빈의 값을 히스토그램에 균등하게 재분배
밝기 분포가 한쪽으로 치우친 유사 영역에서 효과적
CLAHE 알고리즘
- 영상을 타일로 나누어 각 타일의 히스토그램을 계산
- 각 타일의 히스토그램에서 clipLimit보다 큰 값은 전체 반에서 재분배, clipLimit는 히스토그램 크기와 타일의 크기를 고려하여 계산
- 각 타일의 히스토그램 평활화를 수행하고 타일 경계에서 문제를 해결하기 위하여 4개의 이웃 타일의 히스토그램을 이용하여 양선형 보간(bilinear interpolation): HOG와 마찬가지로 계단현상 해결하기 위함
CLAHE (코드)
cv2.createCLAHE를 통해 객체 생성 후 apply로 적용
- cliplimit: 대비 제한 임계값
- tileGridSize: 타일 그리드 크기
예시
- src tileArea: 8*8
- cliplimit: 40, tileGridsize: (1, 1)일 경우, tileArea: 8*8
- 8-비트 그레이스케일 영상에서 histSize는 256이므로
- cliplimit: 40*64/256 = 10임
- tileGridSize는 (1,1)니까 히스토그램은 1개만 계산
- 각 히스토그램에서 clipLimit이 10보다 큰 값은 히스토그램에 균등하게 재분배
- cliplimit: 40, tileGridSize: (2,2)일 경우, 반으로 나눠서 tileArea: 4*4
- cliplimit: 40*16/256 = 2.5
- tileGridSize는 (2,2)니까 히스토그램은 4개를 계산
- 각 히스토그램에서 clipLimit이 2.5보다 큰 값은 히스토그램에 균등하게 재분배
CLAHE 구현
# Python으로 배우는 OpenCV 프로그래밍 예제 5.15
def interpolate(sub_image, UL,UR,BL,BR):
dst = np.zeros(sub_image.shape)
sY, sX = sub_image.shape
area = sX*sY
for y in range(sY):
invY = sY-y
for x in range(sX):
invX = sX-x
val = sub_image[y, x].astype(int)
dst[y,x] = np.floor((invY*(invX*UL[val] + x*UR[val])+\
y*(invX*BL[val] + x*BR[val]) )/area)
return dst
def CLAHE(src, clipLimit = 40.0, tileX = 8, tileY = 8):
histSize = 256
tileSizeX = src.shape[1]//tileX
tileSizeY = src.shape[0]//tileY
tileArea = tileSizeX*tileSizeY
clipLimit = max(clipLimit*tileArea/histSize, 1)
lutScale = (histSize - 1) / tileArea
print("clipLimit=", clipLimit)
LUT = np.zeros((tileY, tileX, histSize))
dst = np.zeros_like(src)
for iy in range(tileY):
for ix in range(tileX):
y = iy*tileSizeY
x = ix*tileSizeX
roi = src[y:y+tileSizeY, x:x+tileSizeX] # tile
tileHist, bins = np.histogram(roi, histSize,[0,256])
if clipLimit > 0: # clip histogram
clipped = 0
for i in range(histSize):
if tileHist[i]>clipLimit:
clipped += tileHist[i] - clipLimit
tileHist[i] = clipLimit
# redistribute clipped pixels
redistBatch = int(clipped/ histSize)
residual = clipped - redistBatch * histSize
for i in range(histSize):
tileHist[i] += redistBatch
if residual != 0:
residualStep = max(int(histSize/residual), 1)
for i in range(0, histSize, residualStep):
if residual> 0:
tileHist[i] += 1
residual -= 1
# calculate Lookup table for equalizing
cdf = tileHist.cumsum()
tileLut = np.round(cdf*lutScale)
LUT[iy, ix] = tileLut
# bilinear interpolation
y = 0
for i in range(tileY+1):
if i==0: # top row
subY = int(tileSizeY/2)
yU = yB = 0
elif i==tileY: # bottom row
subY = int(tileSizeY/2)
yU= yB = tileY-1
else:
subY = tileSizeY
yU = i-1
yB = i
x = 0
for j in range(tileX+1):
if j==0: # left column
subX = tileSizeX//2
xL = xR = 0
elif j==tileX: # right column
subX = tileSizeX//2
xL = xR = tileX-1
else:
subX = tileSizeX
xL = j-1
xR = j
UL = LUT[yU,xL]
UR = LUT[yU,xR]
BL = LUT[yB,xL]
BR = LUT[yB,xR]
roi = src[y:y+subY, x:x+subX]
dst[y:y+subY, x:x+subX] = interpolate(roi,UL,UR,BL,BR)
x += subX
y += subY
return dst
dst2 = CLAHE(src, clipLimit= 40.0, tileX= 2, tileY= 2)
print("dst=\n", dst2)
- 히스토그램을 계산하고 clipLimit보다 큰 히스토그램 빈의 크기의 합을 clipped에 계산
- clipped를 히스토그램에 균일하게 재분배
- 재분배된 히스토그램을 누적시켜서 cdf 계산하고 평활화 변환표 계산 후 LUT에 저장
- LUT를 이용해서 평활화하면 타일 경계 표시가 나타남
- 이를 위해서 양선형 보간
