ML| Decision Tree
Decision Tree에 대해 정리하였습니다.
‘파이썬 머신러닝 완벽가이드(권철민 지음)’, ‘창의적 문제 해결, 서영정 교수님, 2024-2’, Decision Tree란 무엇인가요?, Decision Tree의 Impurity 지표, ID3 알고리즘 설명
Decision Tree
- 분류와 회귀 모두 사용 가능한 지도 학습 모델 중 하나입니다.
- 데이터에 있는 규칙을 학습을 통해 자동으로 찾아내 Tree 기반의 분류 규칙을 만듭니다.
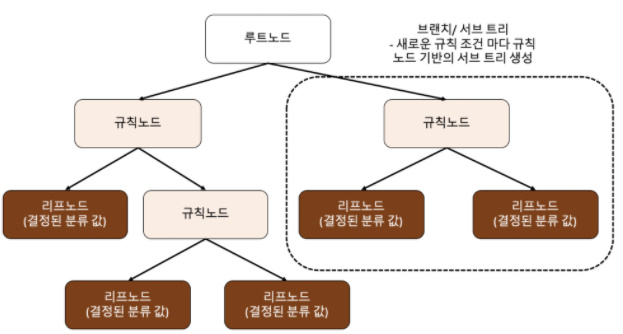
많은 규칙이 있다는 것은 복잡해진다는 것이고 과적합으로 이어지기 쉽습니다. Tree의 depth가 깊어질 수록 성능이 저하될 가능성이 높습니다.
가능한 한 적은 결정 노드로 높은 예측 정확도를 가지려면 데이터를 분류할 때 최대한 많은 데이터 세트가 해당 분류에 속할 수 있도록 결정 노드가 정해져야 합니다. 이를 위해 최대한 균일한 데이터 세트를 구성할 수 있도록 분할하는 것이 필요합니다.
결정 노드는 정보 균일도가 높은 데이터 세트를 먼저 선택할 수 있도록 규칙 조건을 만듭니다. 이러한 정보 균일도를 측정하는 대표적인 방법은 엔트로피를 이용한 정보 이득(Information Gain) 지수와 지니 계수가 있습니다.
Decision Tree의 특징
가장 장점은 ‘균일도’라는 룰을 기반으로 하고 있어서 알고리즘이 쉽고 간단하는 점입니다. 노드들을 시각화할 수 있으며 균일도만 신경쓰면 되서 특별한 경우를 제외하고는 각 피처의 스케일링과 정규화 같은 전처리 작업이 필요 없습니다. 반면 가장 단점은 과적합으로 인해 정확도가 떨어진다는 점입니다. 이를 극복하기 위해 트리의 크기를 사전에 제한하는 튜닝이 필요합니다.
분할 기준 알고리즘: 지니 계수, 정보이득
불순도(Impurity)
- 해당 범주 안에서 서로 다른 데이터가 얼마나 섞여 있는지를 의미합니다. 빨4 & 파1이면 불순도가 낮고, 순도가 높다라고 할 수 있으며 빨3 & 파5이면 불순도가 높고, 순도가 낮다고 할 수 있습니다.
결정 트리는 불순도를 최소화(순도를 최대화)하는 방향으로 학습을 진행합니다.
불순도는 엔트로피, 엔트로피 등을 사용해서 측정합니다.
불순도(Impurity) 지표
엔트로피(Entropy)
불순도를 측정하는 방법 중 하나로, 정보의 불확실성을 측정합니다.
어떤 노드에서 분할 속성을 선택했을 때 정보량을 계산하고 해당 속성 값의 엔트로피를 최소화하는 방향으로 의사결정나무 구조를 만드는데 활용됩니다.
- 낮은 엔트로피 = 경우의 수가 적음 = 낮은 정보량 = 낮은 불확실성 = 낮은 불순도
- 높은 엔트로피 = 경우의 수가 많음 = 높은 정보량 = 높은 불확실성 = 높은 불순도
엔트로피를 측정하는 방법 중에 샤논 공식은 아래와 같습니다.
- D: 데이터 집합
- m: 분류하고자 하는 실제값들의 가짓수
- p_k: k번째 실제값에 해당하는 데이터들의 확률, 엔트로피를 계산하려는 데이터 집합에서 k번째 실제값에 해당하는 데이터의 비율로 계산
속성별 엔트로피
- 속성 A로 분류했을 때 A의 모든 클래스의 각 엔트로피를 계산하고 데이터 개수만큼 가중치를 부여합니다.
- Values(A): 속성 A가 가질 수 있는 값의 집합
- D_v: 속성 A의 값이 v인 데이터의 집합
- |D|: 데이터 집합 D의 크기
지니 계수
지니 계수는 불순도를 측정하는 또 다른 방법으로, 값이 0일수록 해당 노드는 완전히 순수하다고 볼 수 있습니다.
- C: 클래스의 총 개수
- p_i: 클래스 i에 속할 확률
정보이득(information Gain)
Impurity 지표들을 바탕으로 각 node들의 복잡성을 계산할 수 있습니다.
그리고 이 Impurity를 바탕으로, (decision tree에 의해 나누기 전의 Impurity - 나누어진 subset들의 Impurity) 값을 통해 Impurity가 얼마나 개선되었는지 계산할 수 있고, 이를 information gain이라고 합니다.
속성별 정보 이득
- 정보이득이 클수록 속성 A를 기준으로 데이터를 분류했을 때 얻을 수 있는 정보량이 많습니다.
- A를 기준으로 나눌 때 엔트로피가 작으면 해당 속성을 기준으로 데이터를 나누기 좋습니다.
유형
- ID3: 엔트로피와 정보 이득(획득)을 메트릭으로 활용하여 후보 분할을 평가합니다.
- C4.5: 정보 획득 또는 획득 비율을 사용하여 분할 지점을 평가합니다.
- CART: ‘분류 및 회귀 트리’의 약자로 회귀도 가능한 알고리즘입니다. 지니 불순도를 사용하여 분할할 이상적인 속성을 식별합니다. 지니 불순도를 사용하여 평가할 때 값이 낮을수록 이상적입니다.
ID3(Iterative Dichotomiser 3)
성장(grow): 일반적으로 의사결정나무를 생성하는 방법을 ‘성장’이라고 부릅니다. 각 노드에서 엔트로피가 최대로 감소하도록 하는 분할 속성을 결정하는 과정입니다.
ID3: 반복적으로 데이터를 나누는 알고리즘입니다. 탑다운 방식으로 정보이득을 최대화하는 greedy 방식의 최적화 알고리즘입니다. 각 노드마다 반복적으로 계산된 정보이득을 기반으로 노드별 데이터 분류 기준(속성)을 정합니다.
Decision Tree 계산
와인 예제


컴퓨터 구매 여부 예제
| 번호 | 나이(x1) | 수입(x2) | 학생 여부(x3) | 신용 등급(x4) | 구매 여부(y) |
|---|---|---|---|---|---|
| 1 | 청소년 | 고소득층 | 아니오 | 좋음 | 미구매 |
| 2 | 청소년 | 고소득층 | 아니오 | 아주 좋음 | 미구매 |
| 3 | 청년 | 고소득층 | 아니오 | 좋음 | 구매 |
| 4 | 중년 | 중소득층 | 아니오 | 좋음 | 구매 |
| 5 | 중년 | 저소득층 | 예 | 좋음 | 구매 |
| 6 | 중년 | 저소득층 | 예 | 아주 좋음 | 미구매 |
| 7 | 청년 | 저소득층 | 예 | 아주 좋음 | 구매 |
| 8 | 청소년 | 중소득층 | 아니오 | 좋음 | 미구매 |
| 9 | 청소년 | 저소득층 | 예 | 좋음 | 구매 |
| 10 | 중년 | 중소득층 | 예 | 좋음 | 구매 |
| 11 | 청소년 | 중소득층 | 예 | 아주 좋음 | 구매 |
| 12 | 청년 | 중소득층 | 아니오 | 아주 좋음 | 구매 |
| 13 | 청년 | 고소득층 | 예 | 좋음 | 구매 |
| 14 | 중년 | 중소득층 | 아니오 | 아주 좋음 | 미구매 |


Decision Tree 실습
sklearn은 CART(Classification And Regression Trees) 알고리즘 기반입니다.
Decision Tree 파라미터
DeciisonTreeClassifier, DecisionTreeRegressor 모두 파라미터는 다음과 같이 동일한 파라미터를 사용합니다.
- min_samples_split: 노드를 분할하기 위한 최소한의 샘플 데이터 수로 과적합을 제어하는데 사용, 디폴트: 2, 작게 설정할 수록 노드가 많아져서 과적합 가능성 증가
- min_samples_leaf: 말단 노드(leaf)가 되기 위한 최소한의 샘플 데이터 수, min_samples_split과 유사하게 과적합 제어 용도, 그러나 비대칭적 데이터의 경우 데이터가 극도로 작아질 수 있으니 이 경우 작게 설정
- max_fatures: 최적의 분할을 위하 고려할 최대 피처 개수, 디폴트 None, 데이터 세트의 모든 피처를 사용해 분할 수행
- int: 대상 피처의 개수, float: 전체 피처 중 대상 피처의 퍼센트
- ‘sqrt’: 전체 피처 중 sqrt(전체 피처 수), 즉 루트(전체 피처 개수)만큼 선정
- ‘auto’: sqrt와 동일
- ‘log’: 전체 피처 중 log_2(전체 피처 개수)선정
- ‘None’: 전체 피처 선정
- max_depth: 최대 깊이 규정, 디폴트 None, None으로 설정 시 완벽하게 클래스 결정 값이 될 때까지 깊이를 계속 키우며 분할하거나 노드가 가지는 데이터 개수가 min_samples_split보다 작아질 때까지 계속 깊이를 증가시킴, 깊이가 깊어지면 min_samples_split 설정대로 최대 분할하여 과적합되니 제어 필수
- max_leaf_nodes: 말단 노드의 최대 개수
시각화는 Graphviz 패키지를 활용합니다.
실습 코드
from sklearn.tree import DecisionTreeClassifier
from sklearn.metrics import accuracy_score
'''
class sklearn.tree.DecisionTreeClassifier(*, criterion='gini', splitter='best', max_depth=None, min_samples_split=2, min_samples_leaf=1, min_weight_fraction_leaf=0.0, max_features=None,
random_state=None, max_leaf_nodes=None, min_impurity_decrease=0.0,class_weight=None, ccp_alpha=0.0, monotonic_cst=None)
'''
dt_clf = DecisionTreeClassifier(random_state=156)
dt_clf.fit(X_train, y_train)
pred = dt_clt.predict(X_test)
accuracy = accuracy_score(y_test, pred)
직접 구현
import pandas as pd
import numpy as np
from sklearn.model_selection import train_test_split
from sklearn.metrics import accuracy_score
pd_data = pd.read_csv('AllElectronics.csv')
pd_data = pd_data.drop("RID",axis = 1)
print(pd_data)
# 데이터셋을 학습용과 테스트용으로 분리
train_df, test_df = train_test_split(pd_data, test_size=0.3, random_state=42)
# 정보 이득 계산 함수들
def get_info(df):
buy = df[df["class_buys_computer"] == "yes"]
not_buy = df[df["class_buys_computer"] == "no"]
x = np.array([len(buy) / len(df), len(not_buy) / len(df)])
y = np.log2(x[x != 0])
info_all = -sum(x[x != 0] * y)
return info_all
def get_attribute_info(df, attribute_name):
attribute_values = df[attribute_name].unique()
get_infos = []
for value in attribute_values:
split_df = df[df[attribute_name] == value]
get_infos.append((len(split_df) / len(df)) * get_info(split_df))
return sum(get_infos)
# 의사결정 나무 빌드 함수
def build_decision_tree(df, attributes):
if len(df["class_buys_computer"].unique()) == 1:
return df["class_buys_computer"].iloc[0]
if not attributes:
return df["class_buys_computer"].mode()[0]
info_all = get_info(df)
info_gains = []
for attribute in attributes:
attribute_info = get_attribute_info(df, attribute)
info_gain = info_all - attribute_info
info_gains.append((attribute, info_gain))
best_attribute, _ = max(info_gains, key=lambda x: x[1])
tree = {best_attribute: {}}
attribute_values = df[best_attribute].unique()
remaining_attributes = [attr for attr in attributes if attr != best_attribute]
for value in attribute_values:
split_df = df[df[best_attribute] == value]
subtree = build_decision_tree(split_df, remaining_attributes)
tree[best_attribute][value] = subtree
return tree
# 학습 데이터로 의사결정 나무 학습
attributes = ["age", "income", "student", "credit_rating"]
decision_tree = build_decision_tree(train_df, attributes)
# 예측 함수
def predict(tree, sample):
attribute = list(tree.keys())[0]
if sample[attribute] in tree[attribute]:
subtree = tree[attribute][sample[attribute]]
if isinstance(subtree, dict):
return predict(subtree, sample)
else:
return subtree
else:
return "unknown"
# 테스트 데이터에 대한 예측 수행
test_samples = test_df.to_dict(orient="records")
predictions = [predict(decision_tree, sample) for sample in test_samples]
# 정확도 계산
actual = test_df["class_buys_computer"].values
accuracy = accuracy_score(actual, predictions)
print("예측 정확도:", accuracy)
